筆者は大学で経済学を学んでいます。新学年になり他学部の友達に時間割を見せると、「ゲーム理論」って何をするの、と聞かれました。経済学部の学生なら多くの人が学ぶであろうゲーム理論について紹介します。

自分の損得が自分の行動のみならず、他者の行動にも左右されて決まる状況を分析する理論です。つまり、相手の出方を読む必要がある状況で活躍します。この理論では「ナッシュ均衡」という重要な概念が出てきます。これは自分一人だけが戦略を変えても得をしない時の状況を指します。言い換えれば、お互いが最適な戦略を取り合っており、これ以上、変える必要がない状態のことです。では、この理論でコロナ禍のマスク・トイレットペーパー買い占め問題を考えてみたいと思います。

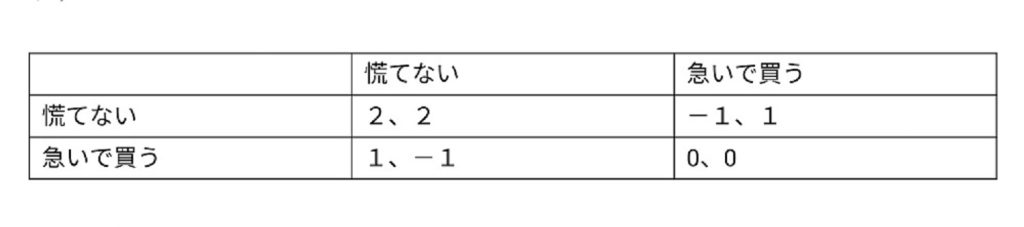
新型コロナウイルスが流行した22年は店頭でのマスクの品薄状態が続き、インターネットでは高額で転売される騒動が起きました。品薄情報は結果的にデマと分かりますが、当時は根拠に乏しい噂話のようなものでした。まず、必要な商品が店頭から消えていくのを見た時に買い急ぎ、多少余分な量を持っておくというのは消費者にとって普通の行動と言えます。そこでAさん（表の縦側）とBさん（表の横側）が品薄時に「慌てない」、「急いで買う」という選択をする場面で考えてみます。

数字は満足度を表しており、お互い「慌てない」場合は自分の好きなタイミングで商品を購入できるので２とします。相手が「慌てない」で自分が「急いで買う」場合は急ぐ分のコストがかかるため、満足度を半分の１とします。お互いが急ぐ場合は品薄状態になるため、買えないリスクが生じます。なので、さらに１を引いた０と仮定します。相手が「急いで買う」、自分が「慌てない」場合はすでに品切れが起きている可能性があるので、Aさんの満足度は－1になりまってしまいます。

（数字は、左側がAさんの満足度、右側がBさんの満足度）

この場合のナッシュ均衡はお互い「慌てない」時とお互い「急いで買う」時です。通常はお互い「慌てない」という選択をしますが、品薄などの情報が広まるとBさんは急いで買うでしょう。この時にAさんは、慌てないままだと－１という損を被るため、対抗して急いで買うのです。

このような買い占め問題が起きている時は、自分一人だけが行動を変えても損をしてしまう結果となります。こういった「わな」から抜け出すためには２人が同時に「慌てない」に変わるしかありません。

その方法としては「マスメディアなどを通じて工場などに在庫があることを２人とも知ること」があげられます。２人とも情報を得ることで「慌てる必要がない」そして「相手も同じ報道を見て同じように思っているだろう」と考えることができます。

ゲーム理論は他にも企業間の価格競争やオークション、政治家の戦略的な行動など幅広い分野を考察することができます。普段の何気ない行動についてもゲーム理論を使って考えてみると思わぬ発見があるかもしれません。

参考記事:

7日付　読売新聞オンライン　米カリフォルニア大バークレー校の鎌田教授が講演「ゲーム理論への招待」…桜蔭（https://www.yomiuri.co.jp/kyoiku/support/information/CO036567/20250502-OYT8T50026/）